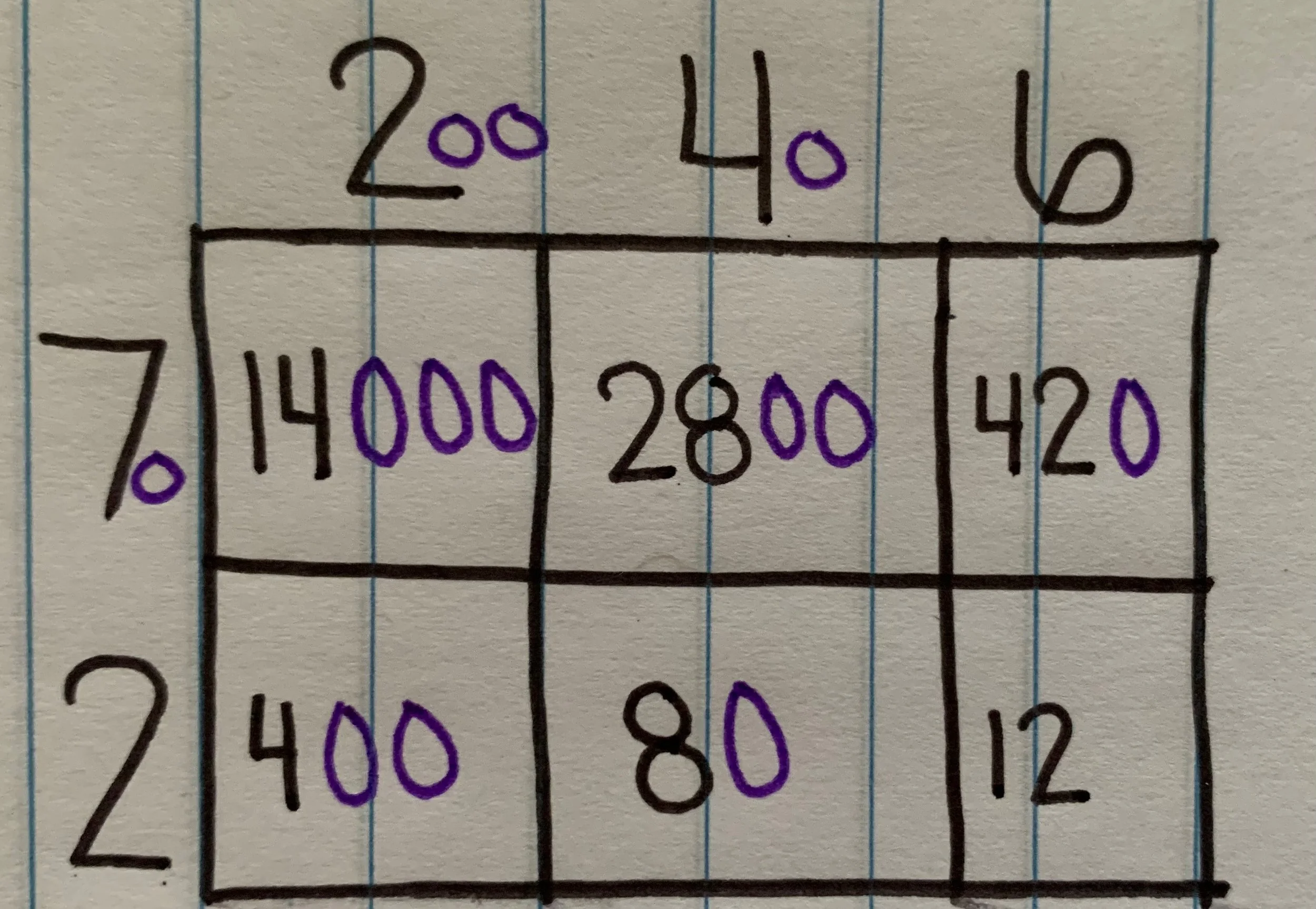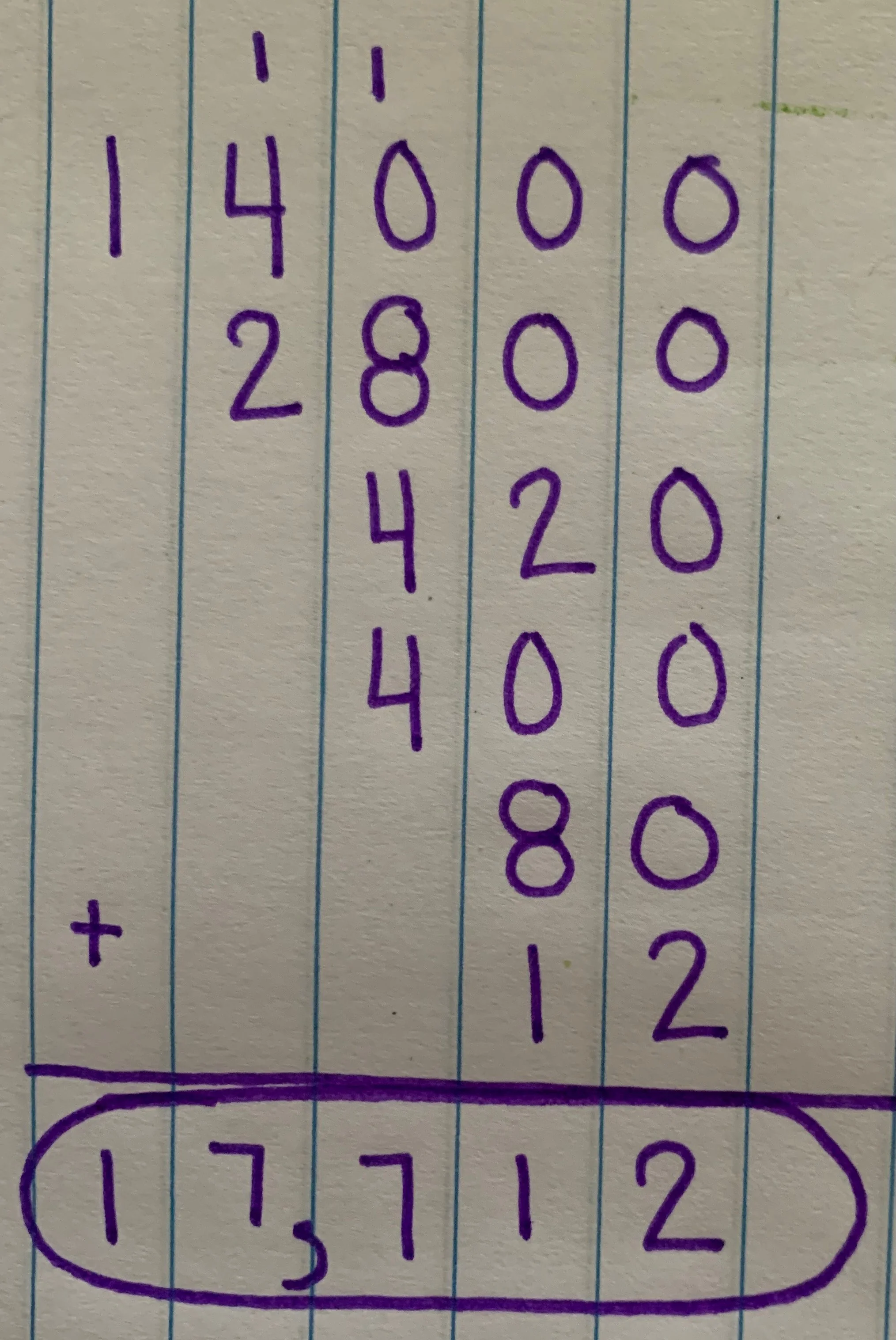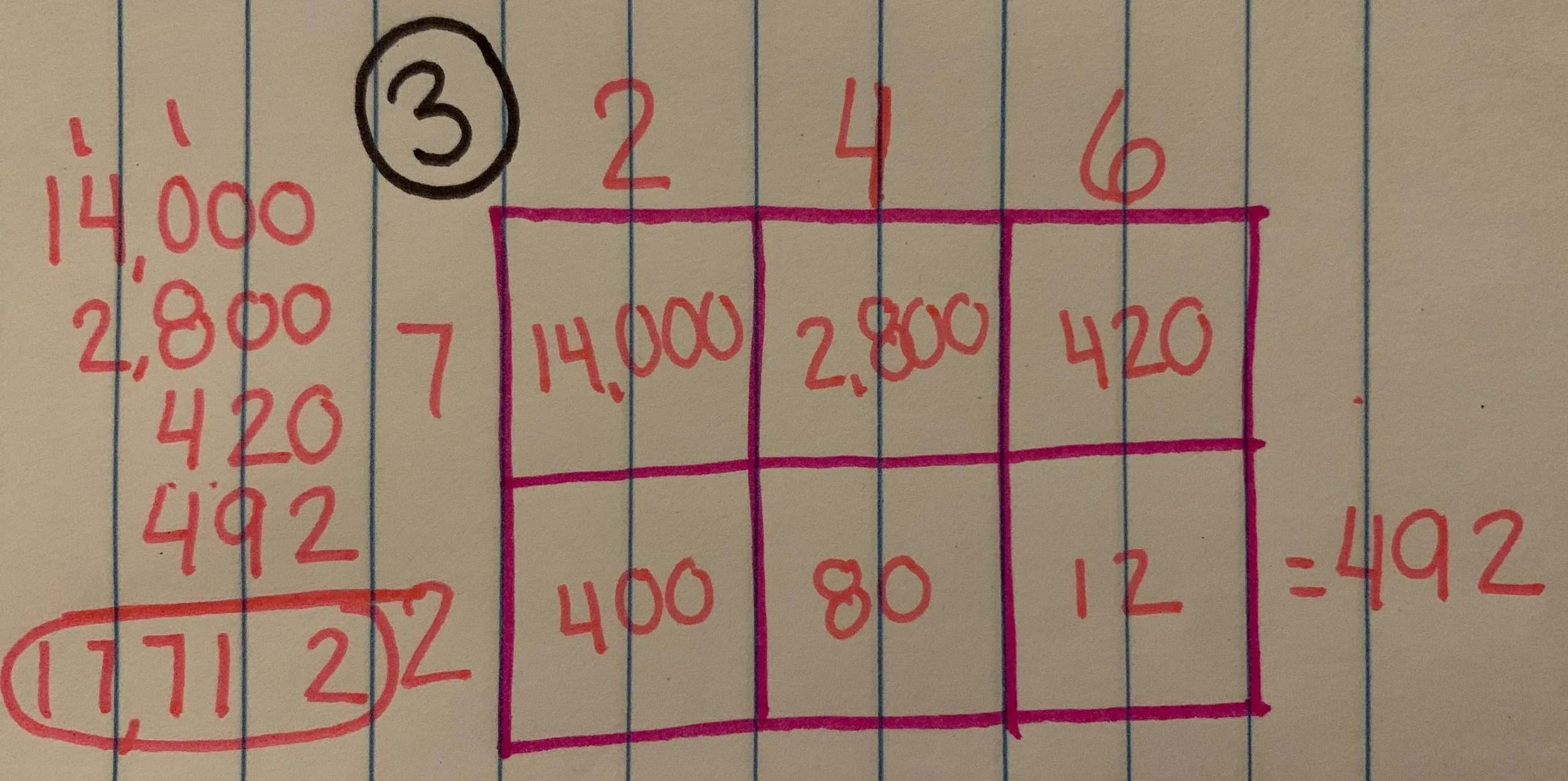What’s the Deal with This New Math?
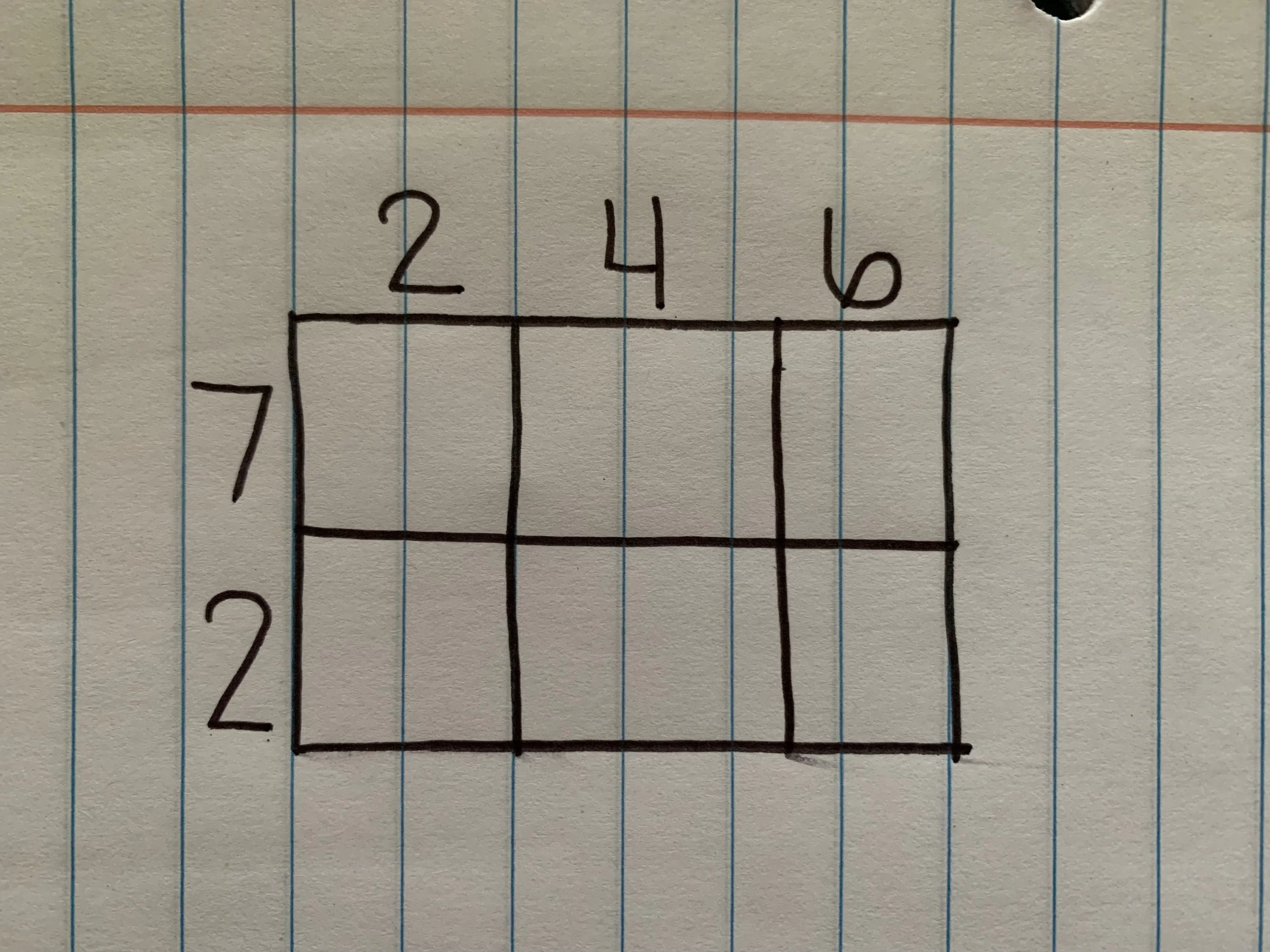
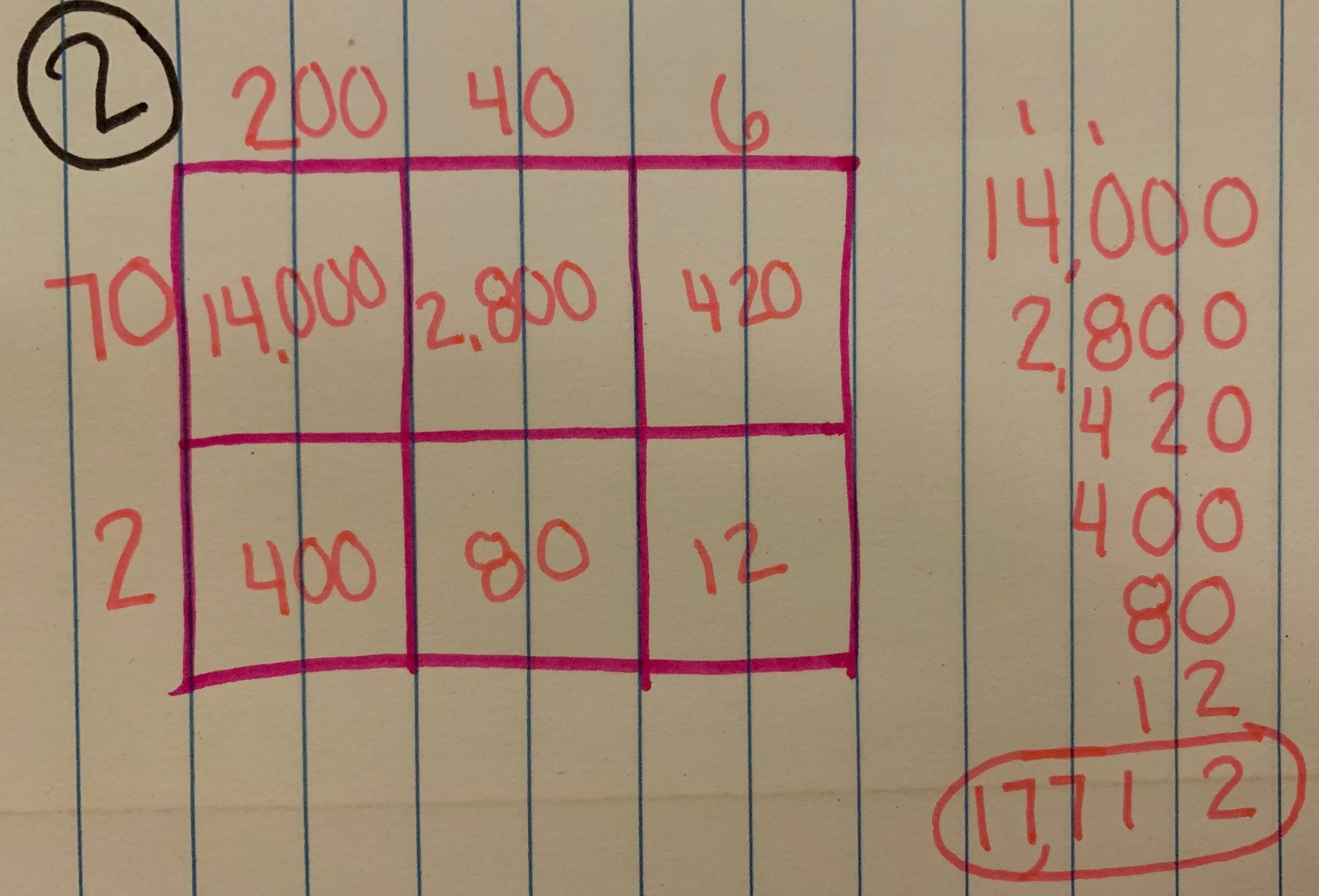
My first teaching job was in 5th grade down in North Carolina. I will never forget the first day of school not only because we had to jump into grade-specific content on us day 1 (we were teaching actual lessons on the first day of school), but also because of the content of those lessons. I had missed the summer planning that the other teachers did to get the first weeks of school plans done, but the plans were provided for me so I initially felt confident and like I would be ok. After all, I went to college for this how bad could it be? If you haven’t already guessed, I was NOT prepared for the box with numbers around it that was supposed to help me multiply. I had never before seen such a thing in all my years in school as a student, or even any of my intern teaching hours. If you still aren’t sure what I am talking about check out the picture below. The object of this is to help students solve 246 x 72. I was so stumped I made it an interactive lesson and asked who wanted to solve the problem on the board so that I could also see how to solve the problem. I also had to use the same strategy to find the art room when it was their specials time because nobody had given the new teachers a tour.
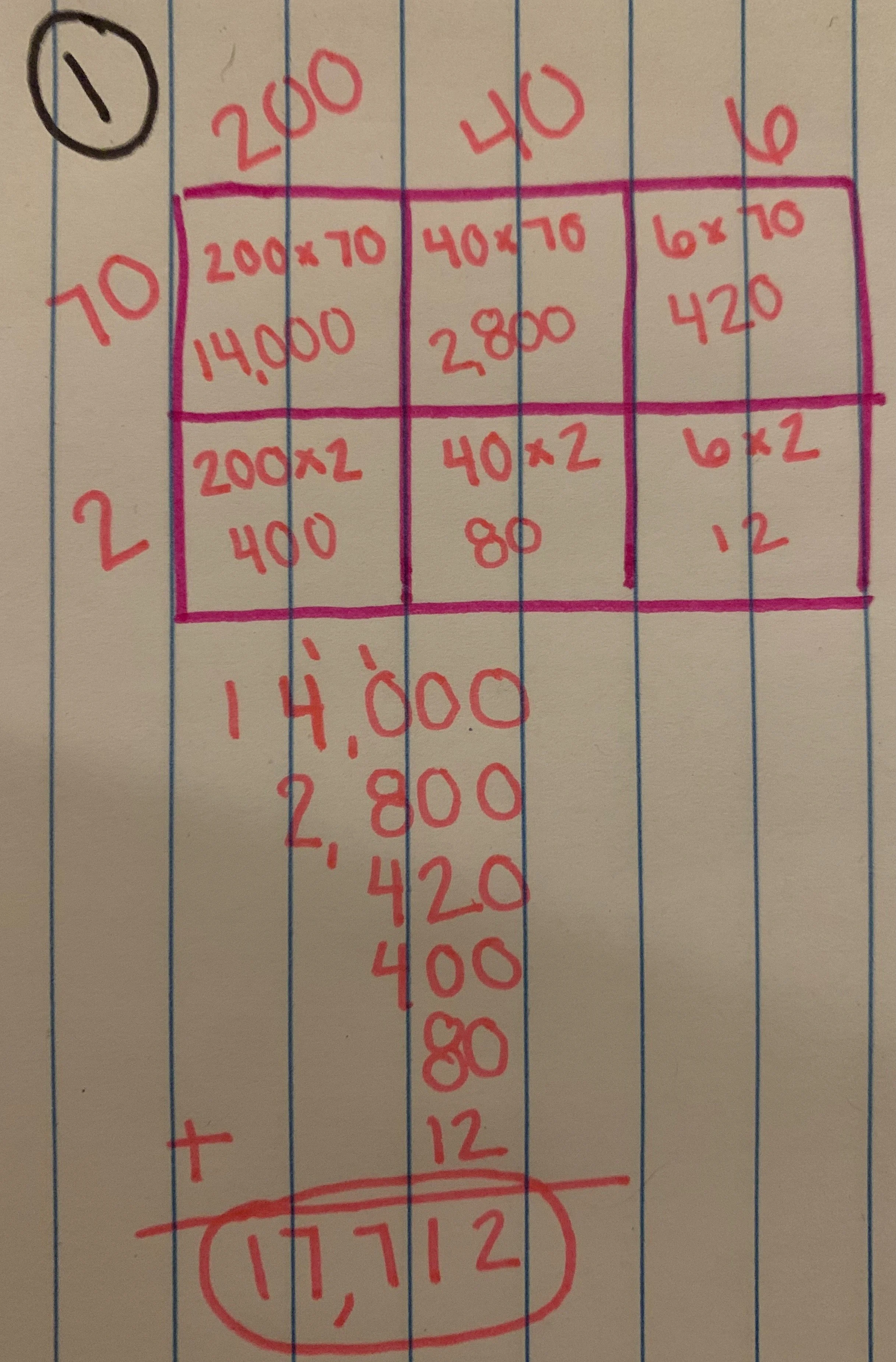
This strategy is one of several that students learn as they develop their understanding of multiplication of multi-digit numbers in 3rd-5th grades. And although I was never taught or trained in this method, I actually came to really love this strategy. It is a longer, more visual version of the distributive property which says that you can essentially take numbers apart based on place value and complete the operations required us to “put it back together” by adding up all the sums. You may still be thinking that this is insane and what’s wrong with the standard algorithm that most people were taught in school. That is a fair question, and there is nothing wrong with the standard algorithm but there is also nothing wrong with any of these other strategies either. When I was a kid, I absolutely hated math and considered myself not good at math, and now it is my favorite subject to teach. The thing that changed for me was the way we are teaching math to students. I never understand the standard algorithm for multiplication or division, and it made so much of math harder than it needed to be. Everything I learned I was taught by a teacher saying that this is the one and only way to solve a problem. Now, looking at this “new” math I am seeing that is not the case. Each of the strategies tie into each other and all will lead you to the correct answer. The question then becomes for the students to pick the one that makes the most sense for them. I have students who prefer the standard algorithm and I allow them to use it as long as they can explain where they are getting their answer from. If students struggle with the standard algorithm, I direct them to this area model strategy or just use the distributive property to solve the problem. I’ve often heard that these “new” ways take longer, and I have to respectfully disagree with people who say that. Any strategy is going to take time when it is new, but once you have had adequate practice these strategies all end up taking roughly the same amount of time. You also learn to develop your own “shortcuts” to solve the problems as you get more comfortable. Below is an example of progression in solving a multiplication problem using the area model strategy. By the time I have gotten to the 3rd stage, I have created several shortcuts, including mentally quickly adding up the bottom row to eliminate some of the possible errors that can come from adding 6 numbers at a time.
This is just one example based on multiplication. If you have a younger student, you will see versions of this using addition and subtraction. Really try to embrace those strategies and remember 2 important things about them:
1. They are transitional strategies that lead to a deeper understanding of the standard algorithm.
2. Developing an understanding of each of the strategies before moving to the next is crucial to making sense of the “next level” operations. Addition and subtraction will lead to multiplication and division.
The new math can be new, scary, confusing, insert adjective here for everyone when they first see it, but if you give it a chance you will see your students really grow and develop a love of math. Keep coming back and checking out the blog for additional posts, tips, and resources. Let me know if there is a specific topic that you would like more information on and I would love to write a post and I am sure other’s out there have the same questions.